Finding Near Optimal Solutions for Complex Real-world Problems

Many real-world problems cannot be solved exactly, even with the use of high-performance computers

Professor Fujito explains that “the use of computers is essential for processing large amounts of data and for solving complex real-world problems. However, in reality, there exists a division between problems that can and cannot be easily solved using computers. When a problem is sufficiently complex, it cannot be solved, even over the course of several years, no matter how powerful the computer used. In fact, countless examples of real-world problems exist that do not yield such simple solutions. In practice, there is no alternative but to adopt a method of providing a solution that is close to the correct one, using approximations. This essentially consists of solving an optimization problem.”

Although the operating capacity of computers has improved exponentially in recent years, these kinds of problems cannot be solved by making ordinary improvements to existing computing capabilities.

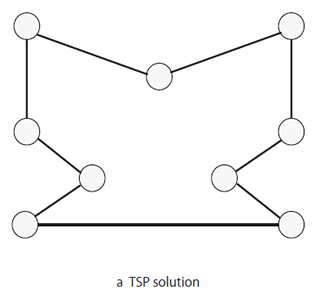
A well-known classic problem is the “traveling salesman problem (TSP)”. This is the problem of finding the shortest route that a salesman can take to visit each of his target customers and return to his company. As long as the number of customers is small, this does not pose any difficulty. However, if the number of visits to be made increases to a few hundred, the number of combinations becomes very large, resulting in an enormous number of calculations. In such cases, the problem becomes unsolvable.

According to Professor Fujito, “a similar problem involves the search for the best product delivery route for convenience stores. Since the products required for each store are different, and the applicable conditions vary, calculations that are much more complex than those of the traveling salesman problem must be solved. Although some industries have already introduced computers in response to these problems, many still rely only on experience. If an optimal solution can be derived with regard to these various problems, the required cost, time, and energy can all be optimized. We have worked on the design of algorithms for such problems.”

In 2005, a group of professors from Carnegie Mellon University who drew up the game schedule for the American Major League created a sensation by significantly reducing the travel distance. Sports scheduling is beset with difficult conditions, such as the need to combine home and away games in the most unbiased manner. Nowadays, computers have been introduced in other sports as well, such as football, because they are able to contribute to the efficiency, while clearly incorporating the various conditions of optimization.

“For example, the task we are currently working on in our laboratory concerns the scheduling of nurses in a hospital. We are trying to create a work schedule that, while incorporating the shift system, provides the best possible combination of veteran and young nurses, and ensures that everyone is able to work without being burdened. Again, this is a discrete optimization problem. In this manner, we are exploring the methodology every day to derive better solutions by utilizing mathematics,” says Professor Fujito.

Formulating and adopting linear programming for NP-hard problems

The origin of the study of discrete optimization problems dates back to World War II, when “Operations Research” was successfully used. This is a research area that was embarked upon in order to improve the efficiency of “logistics,” such as the movement of military troops or distribution of supplies. One of its core techniques is that of “linear programming.”

Professor Fujito describes: “Linear programming is an algorithm that is used to tackle the problem of representing both the objective function and the constraints as linear equations, and is very effective as a framework for formulating optimization problems. Because the input and output are in a linear relationship, or in other words are proportional to each other, the problem is easy to handle mathematically, and a quick and efficient solution can be obtained.

On the other hand, optimization problems, such as the aforementioned traveling salesman problem, are said to be “NP (Non-deterministic Polynomial time) hard” problems, for which a polynomial time (realistic time) algorithm is not likely to be found, and hence they are considered to be difficult to solve. Our aim is somehow to derive an accurate solution, while knowing that this is difficult to achieve. Therefore, we have set our sights on linear programming. In other words, the difficult problem is replaced with a linear programming problem, and a reasonably accurate approximate solution is obtained.”

However, the solution obtained through linear programming is not a discrete solution. As this is a continuous solution, it must be replaced once again with a solution to the discrete optimization problem. The design of algorithms for this step is where the skills of Professor Fujito come into play. He explains

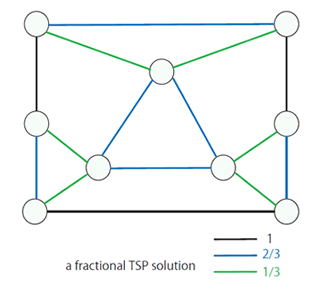
“Besides linear programming, probability theory and fields of discrete mathematics are also used as tools for the design of algorithms. The fields include graph theory, which deals with graphs consisting of sets of vertices and edges; matroids; and submodularity properties of functions,.

“As a result, quite some time ago in 1999, we designed an algorithm for the NP-hard problem of graph theory known as "the Feedback Vertex Set Problem". By using this algorithm, it became possible to obtain an approximate solution at a fast rate, within the factor of two from the minimum solution, even in the case of a large graph.

“In fact, I did not realize at first that this approach is equivalent to using the primal dual method, which is a type of linear programming. However, other researchers pointed out that this can be explained by the mechanism of the primal dual method. Since then, this paper has been cited by many researchers.”

Areas where young researchers can play an active role

Indeed, the vast experience of seasoned researchers has been indispensable, even in coming up with the idea of using linear programming to solve discrete optimization problems. However, a “spark” is also necessary, and the credit for this goes to Professor Fujito. How does this spark occur?

“Individual effort undoubtedly plays a large role in theoretical research, but there are also many occasions when ideas are generated through discussions. Collaborative work between teachers with experience and young researchers is in particular very effective. Ideas emerge from the combination of rich experience and young flexible thinking. Mathematics is an area where young researchers particularly can play an active role. Because the design of algorithms is becoming increasingly important, I would like to see more and more students becoming interested in this world of mathematics,” opines Professor Fujito.

However, not content with merely designing individual algorithms, Professor Fujito mentions that his vision is to continue to focus on the theory of designing algorithms.

Reporter's Note

Professor Fujito actually graduated from the Department of Mechanical Engineering. Being fascinated by computers, he decided to undertake his Master's in Computer Science at an American university.

“While mathematics, which is the foundation of engineering, consists of calculus, linear algebra, complex analysis, etc., the mathematics used in the field of computer science mainly consists of discrete mathematics and probability theory. Subjects such as graph theory are simple but very profound, a very interesting world,” he says, his eyes shining.

The fields of discrete mathematics and applied mathematics, although not very well known in Japan, are essential and cutting-edge fields, whether dealing with big data or on the contrary, predicting future events from small data. The studies of Professor Fujito will become increasingly relevant in this context.

References

• V. Bafna, P. Berman, T. Fujito. (1999). A 2-Approximation Algorithm for the Undirected Feedback Vertex Set Problem, SIAM Journal on Discrete Mathematics, 12, 3, 289-297.
• T. Hibi, T. Fujito. (2015). Multi-Rooted Greedy Approximation of Directed Steiner Trees with Applications, Algorithmica, doi:10.1007/s00453-015-9973-1, Published online: 12 February.